置信区间

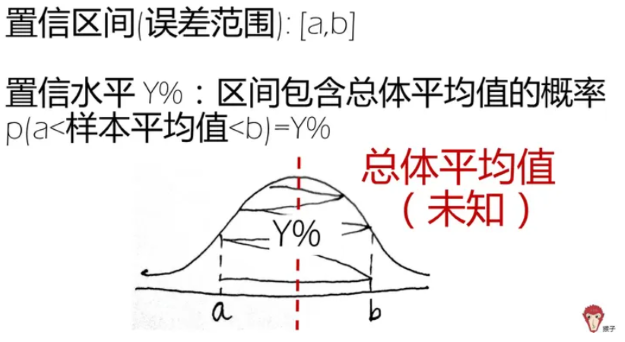
# 置信区间的介绍

参考：https://www.zhihu.com/question/24801731

中心极限定理：样本围绕在总体平均值周围呈现正态分布

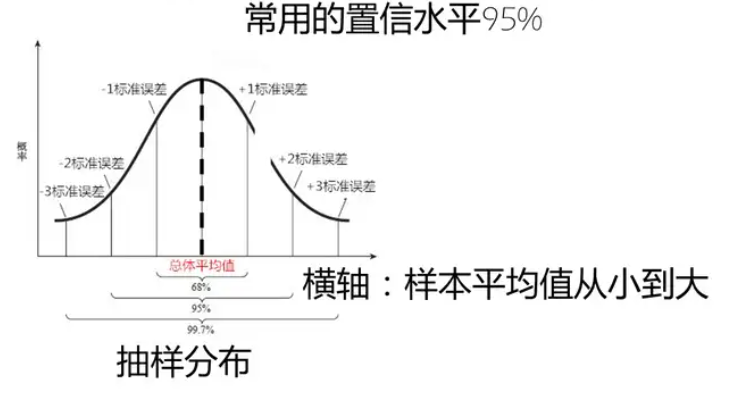
常用置信水平：常用的置信水平是 95%，因为这样可以保证样本的平均值会落在总体平均值 2 个标准误差范围内

大数和小数
当样本大小大于 30 时，抽取的样本符合中心极限定理，也就是抽样分布是正态分布

当样本数量小于 30 时，样本分布符合 T 分布，需要用 T 分布下的置信区间

T 分布参考：https://zhuanlan.zhihu.com/p/39924096

# 回归分析中的置信区间

在最小二乘法中，对线性回归模型 $y = a + bx$ 的系数 $a$ 和 $b$ 的方差可以通过以下推导得到。

# 设定数据

设有 $n$ 个观测点 $(x_i, y_i)$，其中 $i = 1, 2, \ldots, n$。

# 计算系数的估计值

最小二乘法下，系数 $b$ 和 $a$ 的估计值分别为：

$$b = \frac{n \sum (x_i y_i) - \sum x_i \sum y_i}{n \sum (x_i^2) - (\sum x_i)^2}$$

$$a = \bar{y} - b \bar{x}$$

其中：

• $\bar{x} = \frac{1}{n} \sum x_i$
• $\bar{y} = \frac{1}{n} \sum y_i$

# 误差的计算

我们定义误差项 $e_i = y_i - (a + bx_i)$。然后，我们可以计算误差平方和 $SSE$：

$$SSE = \sum e_i^2 = \sum (y_i - (a + bx_i))^2$$

# 方差的推导

方差 $\sigma^2$ 是误差的均方：

$$\sigma^2 = \frac{SSE}{n - 2}$$

# 系数的方差

系数 $a$ 和 $b$ 的方差可以被推导为：

1. 方差 $b$（斜率）

$$Var(b) = \sigma^2 \cdot \frac{1}{\sum (x_i - \bar{x})^2}$$

2. 方差 $a$（截距）

$$Var(a) = \sigma^2 \cdot \left(\frac{1}{n} + \frac{\bar{x}^2}{\sum (x_i - \bar{x})^2}\right)$$

3. 这提供了对于模型参数估计的不确定性的量化。

# 系数的标准差

1. 对于斜率（$b$）的标准误

首先，我们可以从方差的公式计算斜率的标准误：

$$SE(b) = \sqrt{Var(b)} = \sqrt{\sigma^2 \cdot \frac{1}{\sum (x_i - \bar{x})^2}} = \frac{\sigma}{\sqrt{\sum (x_i - \bar{x})^2}}$$

2. 对于截距（$a$）的标准误

然后，我们继续计算截距的标准误：

$$SE(a) = \sqrt{Var(a)} = \sqrt{\sigma^2 \cdot \left(\frac{1}{n} + \frac{\bar{x}^2}{\sum (x_i - \bar{x})^2}\right)}$$

这样我们可以将它进一步分解为：

$$SE(a) = \sigma \cdot \sqrt{\frac{1}{n} + \frac{\bar{x}^2}{\sum (x_i - \bar{x})^2}}$$

3. 更进一步的推导

我们注意到 $\sigma^2 $ 也可以通过 $b$ 的标准误与 $x_i$ 的方差来联系：

$$Var(b) = \sigma^2 \cdot \frac{1}{\sum (x_i - \bar{x})^2} \implies \sigma^2 = Var(b) \cdot \sum (x_i - \bar{x})^2$$

将这个带入到 $ SE (a) $ 中：

$$SE(a) = \sqrt{Var(b) \cdot \sum (x_i - \bar{x})^2} \cdot \sqrt{\frac{1}{n} + \frac{\bar{x}^2}{\sum (x_i - \bar{x})^2}}$$

我们可以将 $\sum (x_i - \bar{x})^2$ 替换为 $\sum x^2 - n \bar{x}^2$，这个公式可以直接得到：

$$SE(a) = SE(b) \cdot \sqrt{\frac{\sum x^2}{n}}$$

# 系数 a 和 b 标准差计算的 python 代码

# 通过最小二乘法拟合曲线，得到斜率和截距

coefficients = np.polyfit(x,y,1)

clock_rate, intercept = coefficients

# 计算残差和 MSE (Mean Squared Error)

residuals = y - np.polyval(coefficients,x)

mse = np.sum(residuals**2)/(len(x)-2)

# 计算标准误差

x_mean = np.mean(x)

# var 计算的是方差，默认的自由度 ddof 是 0，已经除以 len (x) 了，所以乘以 len (x) 恢复

# 效果和 np.sum ((x - x_mean) ** 2) 相当

x_var = np.var(x)*len(x) 

SE_slope = np.sqrt(mse/x_var)

SE_intercept = SE_slope * np.sqrt(np.sum(x**2) / len(x)) # 截距标准

# 某一点的标准差

预测值的标准差（Standard Error of the prediction）表示在给定自变量 $x_i$ 下，因变量 $y$ 的预测值 $\hat{y}_i$ 的变异程度。推导过程如下：

# 线性回归模型

在简单线性回归中，模型的形式为：

$$y_i = a + b x_i + e_i$$

其中：

• $y_i$ 是观察值
• $x_i$ 是自变量
• $a$ 是截距
• $b$ 是斜率
• $e_i$ 是误差项（残差）

# 预测值的计算

对于自变量 $x_i$，其对应的预测值 $\hat{y}_i$ 为：

$$\hat{y}_i = a + b x_i$$

# 预测值的标准误

预测值的标准误描述的是在某个自变量值下，预测的因变量值的不确定性。其计算公式为：

$$SE(\hat{y}_0)=\sqrt{SE(e)^2+SE(\hat{y})^2}$$

其中$SE(e)$ 是模型的标准误差 (基于残差计算) 。$SE(\hat{y})$ 是因自变量$x$ 而引入的误差，计算公式为：

$$SE(\hat{y_i}) = SE(e_i) \cdot \sqrt{1 + \frac{1}{n} + \frac{(x_i - \bar{x})^2}{\sum (x_j - \bar{x})^2}}$$

其中各部分的含义：

• $SE(e_i)$: 残差的标准误，即模型的拟合误差。
• $\bar{x}$: 自变量 $x$ 的均值。
• $n$: 观察值的数量。
• $\sum (x_j - \bar{x})^2$: 自变量 $x$ 的离差平方和，反映了自变量的变异程度。

# 推导过程

计算残差的标准误

首先，残差的标准误（$SE(e)$ 或 $SE(y)$）可以表示为：

$$SE(e) = \sqrt{MSE} = \sqrt{\frac{SSE}{n - p}}$$

• $SSE = \sum (y_i - \hat{y}_i)^2$ 是残差平方和。
• $MSE$ 是均方误差（Mean Squared Error）。
• $p$ 是模型的参数数量（对于简单线性回归，$p = 2$）。

预测值的标准误推导

对于每个预测值 $\hat{y_i}$，标准误的具体推导如下：

1. 引入残差的方差：我们有：

$$\hat{y}_i = a + b x_i$$

对这一形式而言，预测的变异性仅由残差项 $e_i$ 的变异性决定，即：

$$Var(\hat{y_i}) = Var(e_i)$$

而 $Var(e_i) = \sigma^2$，$\sigma^2$ 是模型的错误项（残差）的方差。

2. 预测
   方差计算：

   由线性回归，我们可以知道每个点的预测值的方差可以进一步表达为：

   $$Var(\hat{y_i}) = MSE \cdot \left(1 + \frac{1}{n} + \frac{(x_i - \bar{x})^2}{\sum (x_j - \bar{x})^2}\right)$$

   这里，第一部分是预测的总体变异性，第二部分包括由于样本均值引入的变异性，以及自变量值 $x_i$ 离均值 $\bar{x}$ 的距离引入的变异性。

3. 标准误 $SE(\hat{y_i})$：

   因此，预测值 $\hat{y_i}$ 的标准误为方差的平方根：

   $$SE(\hat{y_i}) = \sqrt{MSE} \cdot \sqrt{1 + \frac{1}{n} + \frac{(x_i - \bar{x})^2}{\sum (x_j - \bar{x})^2}}$$

# 最终结果

综合上述推导，我们得出每个点的预测值 $\hat{y}_i$ 的标准误 $SE(\hat{y_i})$ 的最终公式为：

$$SE(\hat{y_i}) = \sqrt{MSE} \cdot \sqrt{1 + \frac{1}{n} + \frac{(x_i - \bar{x})^2}{\sum (x_j - \bar{x})^2}}$$

# 结果意义

• 第一部分 $\sqrt{MSE}$ 表示整体模型的平均误差。
• 第二部分 $\sqrt{1 + \frac{1}{n}}$ 反映了由于样本均值带来的不确定性。
• 第三部分 $\sqrt{\frac{(x_i - \bar{x})^2}{\sum (x_j - \bar{x})^2}}$ 反映了观察点 $x_i$ 离均值的距离对预测的不确定性的影响。

通过这些步骤，你就能够理解如何推导得出线性回归模型中每个点的预测值的标准误。

# 置信区间

关于置信区间和预测区间的通俗解释见于： 关于回归分析中的置信区间和预测区间

置信区间其实就是从平均值点估计出发的区间估计

要做区间估计，首先得找到$\hat y_0$ 的分布

为方便计算，我们先把$\hat y_0$ 分解为两个不相关的随机变量.

$$\begin{aligned}\hat{y}_{0}&=\hat{a}+\hat{b}x_0\\&=\overline{y}+\hat{b}(x_0-\overline{x})\end{aligned}$$

某一点$y_0$ 的方差

$$\begin{aligned} Var(\hat{y}_{0})& =Var(\overline{y})+Var\{\hat{b}(x_{0}-\overline{x})\} \\ &=Var(\overline{y})+(x_0-\overline{x})^2Var(\hat{b}) \\ &=\left\{\frac1n+\frac{(x_0-\overline{x})^2}{\sum_{i=1}^n(x_i-\overline{x})^2}\right\}\sigma^2 \end{aligned}$$

给定$1-\alpha$ 的置信水平的话，区间估计就是

$$\hat{y}_0\pm t_{\alpha/2}(n-2)\cdot \sigma\sqrt{\frac1n+\frac{(x_0-\overline{x})^2}{\sum_{i=1}^n(x_i-\overline{x})^2}}$$

# 预测区间

预测区间就是从个别值点估计出发的区间估计了。

个别值点估计可以从回归直线来理解

对于某个特定的值$x=x_0$ , 根据估计所得的参数，可以计算$y$ 的个别值的点估计

$$\hat{y}_0=\hat{\beta}_0+\hat{\beta}_1x_0+\epsilon_0$$

这里$\hat{y} _0$ 表示个别值$y_0$ 的估计值

因为$y_{0}$ 是包含一个随机误差项，所以$\hat{y}_{0}$ 实际上应该是包含$\epsilon_0.$

只是，在计算$y_{0}$ 估计值的时候，默认$\epsilon_0=0$ 罢了.

目前右边多了一个误差项，这个误差项是一个随机变量.

也就是说，因为看问题的视角不同，一个是平均值角度，一个是个别值角度，所以两个公式左边的$\hat{y}_0$ 含义不同，对应的分布也不同

在个别值估计的视角，计算$\hat{y}_0$ 的方差

$$\begin{aligned}Var(\hat{y}_{0})&=Var(\overline{y})+Var\{\hat{\beta}_1(x_0-\overline{x})\}+Var(\epsilon_0)\\&=Var(\overline{y})+(x_0-\overline{x})^2Var\hat{\beta}_1+Var(\epsilon)\\&=\left\{1+\frac1n+\frac{(x_0-\overline{x})^2}{\sum_{i=1}^n(x_i-\overline{x})^2}\right\}\sigma^2\end{aligned}$$

给定$1-\alpha$ 的置信水平的话，区间估计就是

$$\hat{y}_0\pm t_{\alpha/2}(n-2)\cdot \sigma\sqrt{1+\frac1n+\frac{(x_0-\overline{x})^2}{\sum_{i=1}^n(x_i-\overline{x})^2}}$$

# python 代码同时绘制出最小二乘拟合的置信区间和预测区间

import numpy as np

import matplotlib.pyplot as plt

from scipy import stats

# 创建示例数据

np.random.seed(0)

x = np.linspace(0, 10, 100)

y = 2.5 * x + 1 + np.random.normal(0, 2, size=x.shape)  # 真实关系 + 噪声

# 最小二乘法线性回归拟合

A = np.vstack([x, np.ones(len(x))]).T

slope, intercept = np.linalg.lstsq(A, y, rcond=None)[0]

# 预测值

y_pred = slope * x + intercept

# 计算残差

residuals = y - y_pred

std_residuals = np.std(residuals)

# 计算置信区间和预测区间

n = len(x)

t_inv = stats.t.ppf(0.975, df=n-2)  # 95% 置信区间

# 置信区间的标准误差

se_conf = std_residuals * np.sqrt(1/n + (x - np.mean(x))**2 / np.sum((x - np.mean(x))**2))

# 上下置信区间

conf_upper_bound = y_pred + t_inv * se_conf

conf_lower_bound = y_pred - t_inv * se_conf

# 预测区间的标准误差

se_pred = std_residuals * np.sqrt(1 + 1/n + (x - np.mean(x))**2 / np.sum((x - np.mean(x))**2))

# 上下预测区间

pred_upper_bound = y_pred + t_inv * se_pred

pred_lower_bound = y_pred - t_inv * se_pred

# 绘制结果

plt.figure(figsize=(12, 6))

plt.scatter(x, y, label='数据点', color='blue', alpha=0.5)

plt.plot(x, y_pred, label='拟合线', color='red', linewidth=2)

plt.fill_between(x, conf_lower_bound, conf_upper_bound, color='red', alpha=0.3, label='95% 置信区间')

plt.fill_between(x, pred_lower_bound, pred_upper_bound, color='green', alpha=0.3, label='95% 预测区间')

plt.title('最小二乘法线性回归及置信区间和预测区间')

plt.xlabel('自变量 x')

plt.ylabel('因变量 y')

plt.legend()

plt.grid()

plt.show()

# 协方差矩阵求解系数标准差和直接求解的等价性

为了求解线性回归模型 $y = a + bx$ 的系数的标准差，我们首先需要确定模型的参数，再构建协方差矩阵，最后从协方差矩阵中提取出参数 $a$ 和 $b$ 的标准差。以下是每一步的详细推导。

# 线性回归模型

考虑线性回归模型：

$$y = a + bx + \epsilon$$

其中 $\epsilon$ 是误差项，通常假设其满足独立同分布，且均值为 0。

# 设计矩阵

对于模型 $y = a + bx$，我们可以构建设计矩阵 $X$：

$$X = \begin{bmatrix} 1 & x_1 \\ 1 & x_2 \\ \vdots & \vdots \\ 1 & x_n \\ \end{bmatrix}$$

# 参数的估计

采用最小二乘法可以得到参数的估计：

$$\hat{\beta} = (X^T X)^{-1} X^T y$$

其中：

• $\hat{\beta} = \begin{bmatrix} \hat{a} \\ \hat{b} \end{bmatrix}$

# 求解协方差矩阵

协方差矩阵的理解：https://www.zhihu.com/tardis/zm/art/37609917?source_id=1005

1. 计算 $X^T X$：

$$X^T X = \begin{bmatrix} n & \sum x_i \\ \sum x_i & \sum x_i^2 \end{bmatrix}$$

2. 计算 $(X^T X)^{-1}$：

为了计算其逆，可以使用公式：

$$(X^T X)^{-1} = \frac{1}{\text{det}(X^T X)} \cdot \text{adj}(X^T X)$$

其中行列式 $\text{det}(X^T X)$ 为：

$$\text{det}(X^T X) = n \sum x_i^2 - \left( \sum x_i \right)^2$$

因此，逆矩阵为：

$$(X^T X)^{-1} = \frac{1}{n \sum x_i^2 - \left( \sum x_i \right)^2} \begin{bmatrix} \sum x_i^2 & -\sum x_i \\ -\sum x_i & n \end{bmatrix}$$

3. 求取协方差矩阵：

在这个模型中，协方差矩阵公式为：

$$\text{Cov}(\hat{\beta}) = \sigma^2 (X^T X)^{-1}$$

其中 $\sigma^2$ 是误差的方差，可以通过计算残差平方和并除以自由度得到：

$$\sigma^2 = \frac{SSE}{n - p}$$

这里，$SSE = \sum (y_i - \hat{y}_i)^2$，而 $p$ 是模型参数的数量（这里 $p = 2$）。

# 从协方差矩阵求出 $a$ 和 $b$ 的标准差

因为协方差矩阵为：

$$\text{Cov}(\hat{\beta}) = \sigma^2 (X^T X)^{-1}$$

所以，

$$\text{Cov}(\hat{\beta}) = \sigma^2 \cdot \frac{1}{n \sum x_i^2 - \left( \sum x_i \right)^2} \begin{bmatrix} \sum x_i^2 & -\sum x_i \\ -\sum x_i & n \end{bmatrix}$$

具体值为：

1. $\hat{a}$ 的方差：

$$Var(\hat{a}) = \sigma^2 \cdot \frac{\sum x_i^2}{n \sum x_i^2 - \left( \sum x_i \right)^2}$$

2. $\hat{b}$ 的方差：

$$Var(\hat{b}) = \sigma^2 \cdot \frac{n}{n \sum x_i^2 - \left( \sum x_i \right)^2}$$

然后，标准差可以通过取平方根得到：

1. $\hat{a}$ 的标准差：

$$SE(\hat{a}) = \sqrt{Var(\hat{a})} = \sqrt{\frac{\sigma^2 \cdot \sum x_i^2}{n \sum x_i^2 - \left( \sum x_i \right)^2}}$$

2. $\hat{b}$ 的标准差：

$$SE(\hat{b}) = \sqrt{Var(\hat{b})} = \sqrt{\frac{\sigma^2 \cdot n}{n \sum x_i^2 - \left( \sum x_i \right)^2}}$$

# 总结

通过以上步骤，我们得到了从回归模型推导出参数 $a$ 和 $b$ 的标准差的方法。具体步骤包括构建设计矩阵、计算 $X^T X$ 及其逆矩阵、构建协方差矩阵，并从中提取出系数的标准差。这样，我们可以量化参数估计的不确定性。

# python polyfit 的协方差求解和手动求解系数方差对比

numpy 中使用 polyfit 求解协方差矩阵、手动计算标准差、或者 numpy 中的 cov 好像都不一样，暂时统一为使用 polyfit 中的协方差矩阵作为系数误差

关于 polyfit 协方差矩阵的使用见于

https://astro-330.github.io/Lab4/Lab4_solutions.html

https://stackoverflow.com/questions/27757732/find-uncertainty-from-polyfit

https://sachinashanbhag.blogspot.com/2019/10/parameter-uncertainty-in-numpy-polyfit.html

https://github.com/numpy/numpy/blob/main/numpy/lib/_polynomial_impl.py#L449-L695

源码注释中也说到 The covariance matrix of the polynomial coefficient estimates，即是参数误差的估计

import numpy as np

# 示例数据

x = np.array([1, 2, 3, 4, 5])  # 自变量

y = np.array([2, 3, 5, 7, 11])  # 因变量

# 使用 polyfit 进行线性回归拟合

coefficients, cov = np.polyfit(x, y, 1, cov=True)

# 提取系数 a 和 b

a = coefficients[1]  # 截距

b = coefficients[0]  # 斜率

############### 协方差计算标准误差

std_errors = np.sqrt(np.diag(cov))

# 打印结果

print(f'系数 a (截距): {a:.4f}, 标准差: {std_errors[1]:.4f}')

print(f'系数 b (斜率): {b:.4f}, 标准差: {std_errors[0]:.4f}')

############### 手动求解系数方差

# 计算残差和 MSE

residuals = y - np.polyval(coefficients,x)

mse = np.sum(residuals**2)/(len(x)-2)

# 计算标准误差

x_mean = np.mean(x)

x_var = np.var(x,ddof=0)*len(x)

std_errors[0] = np.sqrt(mse/x_var)

std_errors[1] = SE_slope * np.sqrt(np.sum(x**2) / len(x)) # 截距标准误差

# 打印结果

print(f'系数 a (截距): {a:.4f}, 标准差: {std_errors[1]:.4f}')

print(f'系数 b (斜率): {b:.4f}, 标准差: {std_errors[0]:.4f}')

# 输出结果

系数 a (截距): -1.0000, 标准差: 1.0132

系数 b (斜率): 2.2000, 标准差: 0.3055

系数 a (截距): -1.0000, 标准差: 1.0132

系数 b (斜率): 2.2000, 标准差: 0.3055

# 数据本身的置信区间和最小二乘拟合区间的置信区间

数据本身的置信区间和最小二乘曲线的置信区间是两个概念，它们反映的是不同的统计特性，因此通常情况下会有差别。

# 数据本身的置信区间

• 含义：数据本身的置信区间通常是指某个统计量（如均值、比例等）的置信区间，例如一个样本均值的 95% 置信区间，表示在给定的置信水平下，样本均值估计的整体真实均值的可能范围。
• 计算：通常基于样本数据计算，涉及到数据的变异性和样本大小。此置信区间反映了数据在一定置信水平下的不确定性。

# 最小二乘曲线的置信区间

• 含义：最小二乘曲线的置信区间通常指的是回归模型的参数（即回归系数）的置信区间，或者是在特定的自变量水平下，因变量的预测值的置信区间。
• 计算：基于回归模型的残差、标准误差和设计矩阵，通常会产生回归系数的区间估计和因变量在特定自变量值下的预测标准误差，反映了模型估计的不确定性。

# 可能的差异

• 不同的计算基础：数据本身的置信区间计算依赖于样本的均值、标准差，而最小二乘曲线的置信区间则依赖于回归模型的结构、残差和协方差分析。
• 反映的性质不同：
  • 数据本身的置信区间反映的是样本对总体的估计不确定性。
  • 最小二乘回归的置信区间反映的是模型对因变量预测的精准性和回归系数的不确定性。
• 复杂性和变化性：如果数据存在较大的噪声或离群点，数据本身的置信区间会显得较宽，而最小二乘曲线会试图通过拟合数据来减小这种不确定性，可能导致曲线的置信区间相对更窄或更有针对性。

# 示例

例如，假设我们想分析身高与体重的关系。我们可以得到身高的样本均值和 95% 置信区间（如 150 cm 至 170 cm），但通过回归建立模型后，可能会基于特定的身高值（如 160 cm）计算该身高下体重的预测值及其置信区间（如 53 kg 至 67 kg）。

# 大小差异

在大多数情况下，数据本身的置信区间和最小二乘曲线的置信区间不会重叠或会有较大差异，这取决于：

• 数据的分布。
• 模型的拟合程度。
• 数据中的噪声和异常值。

# 总结

数据本身的置信区间和最小二乘曲线的置信区间是基于不同的统计概念和方法计算的。通常情况下，它们之间会出现差异，而这种差异反映了数据的真实状况、模型的表现和不确定性。针对具体问题和数据，理解这两者的关系和不同是重要的。

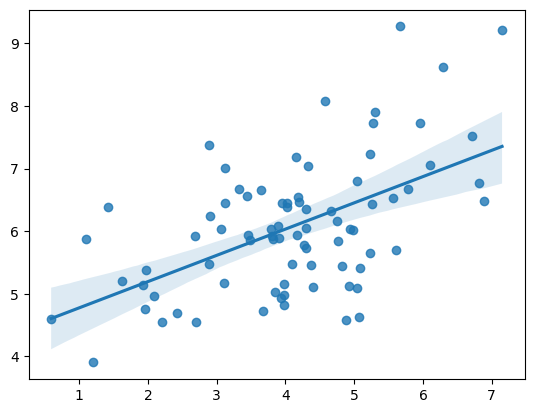
# 绘制线性回归分析的置信区间 —— 调用 seaborn 画图

# https://www.zhihu.com/question/425566655/answer/1524420211

# Import standard packages

import seaborn as sns

import numpy as np

import matplotlib.pyplot as plt

# Set time seed

np.random.seed(8)

# Generate data

mean, cov = [4, 6], [(1.5, .7), (.7, 1)]

x, y = np.random.multivariate_normal(mean, cov, 80).T

# Plot figure

ax = sns.regplot(x=x, y=y, ci=95)

plt.show()

# 绘制一组抽样的置信区间

# 调用 scipy.stats

import scipy.stats as st

alpha = 0.95        # 置信水平

df = 20 - 1         # 自由度

loc = 5             # 均值

scale = 2           # 标准差

# 计算置信区间

confidence_interval = st.t.interval(alpha, df, loc, scale)

print(confidence_interval)

(0.813951891183474, 9.186048108816525)

# 数据量远大于 30 和小于 30 的区别

# https://blog.csdn.net/Lyndon0_0/article/details/108664901

#!/usr/bin/env python3

# -*- coding: UTF-8 -*-

# @Date : 2023/9/20 10:46

# @Author : HELIN

"""

计算95%置信区间：

如果样本量远大于30，三种方法计算结果基本一致；

如果样本量小于30，三种方法计算结果不一致。

备注：方法二和方法三计算结果一致

参考：https://blog.csdn.net/book_dw5189/article/details/130895607

"""

from scipy import stats

import numpy as np

data = np.random.random(1000)  # 随机数

#print ("data:", data.tolist ()[:100])  # 取前 100 个值查看

mean = np.mean(data)  # 均值

std_error = stats.sem(data)  # 标准误差

# 方法一：在处理较小的数据集时可以使用 t 分布方法，通常当数据的元素小于 30 个时 (n<30)

lower, upper = stats.t.interval(0.95, len(data) - 1, loc=mean, scale=std_error)

print(f"方法一: ({lower}, {upper})")

# 方法二：元素的数量超过 30 (n>30)

lower, upper = stats.norm.interval(0.95, loc=mean, scale=std_error)

print(f"方法二: ({lower}, {upper})")

# 方法三：元素的数量超过 30 (n>30)

lower = mean - stats.norm.ppf(0.975) * std_error  # stats.norm.ppf(0.975) ~ 1.96

upper = mean + stats.norm.ppf(0.975) * std_error

print(f"方法三: ({lower}, {upper})")

方法一: (0.47656675317925623, 0.5119764035646733)
方法二: (0.47658820347642394, 0.5119549532675056)
方法三: (0.47658820347642394, 0.5119549532675056)

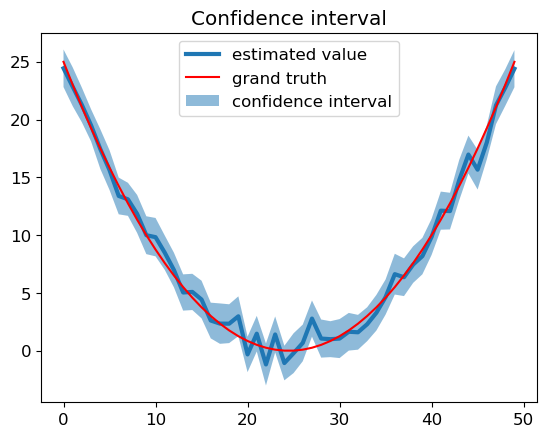
# 尝试以每组抽样的置信区间来解释线性回归的置信区间

1. 以一行值为基础，在每个值上加入正态分布的波动

2. 每个值产出 100 个随机值，形成一组抽样，计算抽样的置信区间

3. 如此便形成了 50 个不同的置信区间，绘制如下图

4. 线性回归分析中的置信区间的产生应该与此类型，由于通过最小二乘估出来的参数 (主要是斜率) 具有一定分布，和自变量相关，所以每一点都有不同的置信区间

# https://blog.csdn.net/weixin_39679367/article/details/114631706

import seaborn as sns

import matplotlib.pyplot as plt

import matplotlib

import numpy as np

import scipy.stats as st

matplotlib.rcParams.update({'font.size': 12})

# 生成数据集

data_points = 50

sample_points = 10000

Mu = (np.linspace(-5, 5, num=data_points)) ** 2 # 数学期望值

Sigma = np.ones(data_points) * 8 # 标准差，即方差的平方根

data = np.random.normal(loc=Mu, scale=Sigma, size=(100, data_points))

# loc: 正态分布的均值，对应着分布的中心，每个元素代表每一行的分布中心

# scale: 正态分布的标准差，对应分布的宽度，scale 越大，正态分布的曲线越矮胖

# size: 多少行，多少列

# 数学期望值和计算置信区间

predicted_expect = np.mean(data, 0) 

# 对 (100,50) 的矩阵求期望值，变为 (1,50)

# 0 表示沿着第一个轴（即行）计算均值，返回每一列的均值

low_CI_bound, high_CI_bound = st.t.interval(0.95, data_points - 1,

                                            loc=np.mean(data, 0),

                                            scale=st.sem(data))

# 处理较小数据集时使用 t 分布方法，通常当元素小于 30 个时

# scale 不是标准差，而是标准误差，st.sem 计算数组平均值的标准误差。

# 即 standard error of the mean，简称 SEM，SEM=s/sqr (n)，其中 s 是标准差，n 是样本大小

# 绘制置信区间

x = np.linspace(0, data_points - 1, num=data_points)

plt.plot(predicted_expect, linewidth=3., label='estimated value')

plt.plot(Mu, color='r', label='grand truth')

plt.fill_between(x, low_CI_bound, high_CI_bound, alpha=0.5,

                label='confidence interval')

plt.legend()

plt.title('Confidence interval')

plt.show()

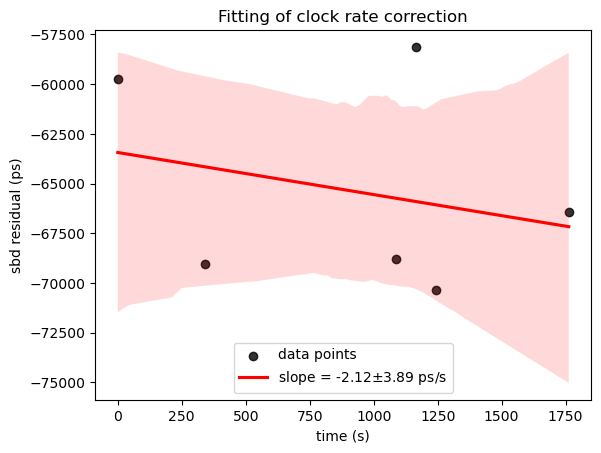
# 实例：拟合直线，并绘制置信区间 + 斜率、截距误差

# https://geek-docs.com/numpy/numpy-ask-answer/289_numpy_how_to_find_error_on_slope_and_intercept_using_numpypolyfit.html

# https://blog.csdn.net/frank_haha/article/details/121271872#:~:text=import%20sea

import numpy as np

import seaborn as sns

import matplotlib.pyplot as plt

time_array = np.array([0, 341, 1087, 1165, 1244, 1762])

sbd_array = np.array([-5.97140007e-08, -6.90215006e-08, -6.87879995e-08, -5.81250004e-08, -7.03634992e-08, -6.64499998e-08])*(10**12)

# 通过最小二乘法拟合曲线，得到斜率和截距

coefficients = np.polyfit(time_array,sbd_array,1)

clock_rate, intercept = coefficients

# 计算残差

residuals = sbd_array - np.polyval(coefficients, time_array)

# 计算 MSE

mse = np.sum(residuals**2) / (len(time_array) - 2)

# 计算标准误差

time_mean = np.mean(time_array) # 平均值

time_var = np.var(time_array)*len(time_array) # 方差

SE_slope = np.sqrt(mse / time_var) # 斜率标准误差

SE_intercept = SE_slope * np.sqrt(np.sum(time_array**2) / len(time_array)) # 截距标准误差

# # 如果是科学计数法表示，可以按照如下内容表示出误差

# slope_formatted = '{:.2e}'.format(clock_rate)

# slope_significant, exponent = slope_formatted.split('e')

# std_adjusted = '{:.2f}'.format(SE_slope / 10**float(exponent))

# my_lable ='slope = ' + f'({slope_significant}$\pm${std_adjusted})e{exponent}' + ' ps/s'

# 普通表示误差

my_lable ='slope = ' +  '{:.2f}$\pm${:.2f}'.format(clock_rate,SE_slope) + ' ps/s'

plt.figure()

sns.regplot(x=time_array, y=sbd_array, ci=95,label='data points', color="black", line_kws={'label': my_lable,'color':'r'})

plt.xlabel('time (s)')

plt.ylabel('sbd residual (ps)')

plt.title('Fitting of clock rate correction')

plt.legend(loc='lower center') # 显示图例

# 输出拟合直线的斜率和截距的标准误差

print('斜率的标准误差为：', SE_slope)

print('截距的标准误差为：', SE_intercept)

斜率的标准误差为： 3.8931638128123027
截距的标准误差为： 4296.39481991996